Thermal Resistance Calculator

2022

This calculator determines the heat flow and heat flux through a homogeneous plate as well as its absolute thermal resistance and R-value.

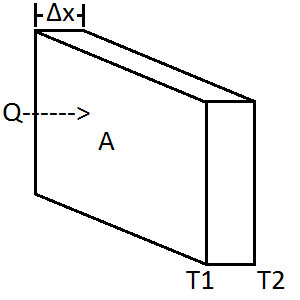
Illustration of Parameters

Calculator

The default is 1" extruded polystyrene foam insulation.

Common Materials

Material	Thermal Resistance (\(W/(m \cdot k)\))
Diamond	2200
Silver	406
Copper	385
Aluminum	205
Epoxy	0.3
Fiberglass Batting	0.043
Extruded Polystyrene	0.0289

Equations

The equation for thermal resistance can be derived from Fourier's law:

\[\frac{\partial Q}{\partial t}=-k∯_S \nabla T \cdot dS\tag{1}\]

Which for a 1D homogeneous plate can be simplified to:

\[\frac{Q}{\Delta t}=P=-kA\frac{\Delta T}{\Delta x}\tag{2}\]

Where \(Q\) is heat in Joules, \(\Delta t\) is time in seconds, \(P\) is power in Watts, \(k\) is conductivity in \(W/(m \cdot k)\), A is area in \(m^2\), \(\Delta T\) is temperature difference between the two sides of the plate in kelvin, and \(\Delta x\) is the thickness of the material in meters. This is the equation used for heat flow.

For heat flux which is power per area, the equation is:

\[Φ_q=-kA\frac{\Delta T}{\Delta x}\tag{3}\]

Absolute thermal resistance tells you how much temperature will rise for a given heat input. This is useful for finding the temperature rise of electrical parts where you often see junction to case thermal resistance in degrees C per W:

\[θ=\frac{\Delta x}{k\cdot A}\tag{4}\]

R-value is the absolute thermal resistance per square meter of a material. This is often used for specifying insulation for building construction where it can be used to compare the effectiveness of different insulations. For example, two inch styrofoam rigid insulation has an R-value of 10 and 3.5 inches of fiberglass batting has an R-value of 13.

\[R_{val}=\frac{\Delta x}{k}\tag{5}\]